
Author: eeeditor

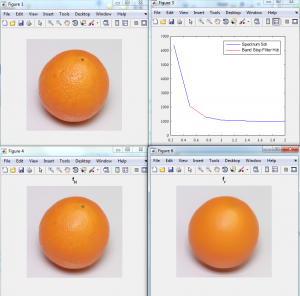
Spectral Total Variation
Matlab code for spectral total variation filtering for grayscale and color images. Here a band-stop example is shown (removing selected bands of textures).
Code for grayscale Spectral TV
Run: demo_ss_freq_tv_texture.m
or
demo_specTV_color_orange.m
Introduction to Medical Imaging 046831 (Spring)

Variational Methods in Image Processing 049064 (Fall)
Digital Signal Processing 046745 (Fall)

Energy Dissipating Flows for Solving Nonlinear Eigenpair Problems
Ido Cohen, Guy Gilboa, “Energy dissipating flows for solving nonlinear eigenpair problems”, Journal of Computational Physics 375 (2018), 1138-1158.
This work is concerned with computing nonlinear eigenpairs, which model solitary waves and various other physical phenomena. We aim at solving nonlinear eigenvalue problems of the general form
$T(u)=\lambda Q(u)$. In our setting $T$ is
a variational derivative of a convex functional (such as the Laplacian operator with respect to the Dirichlet energy),
$Q$ is an arbitrary bounded nonlinear operator and $\lambda$ is an unknown (real) eigenvalue.
We introduce a flow that numerically generates an eigenpair solution by its steady state.
Analysis for the general case is performed, showing a monotone decrease in the convex functional throughout the flow.
When $T$ is the Laplacian operator, a complete discretized version is presented and analyzed. We implement our algorithm on \ac{KdV} and \ac{NLS} equations in one and two dimensions.
The proposed approach is very general and can be applied to a large variety of models. Moreover, it is highly robust to noise and to perturbations in the initial conditions, compared to classical Petiashvili-based methods.
Tags: eigenpairs , nonlinear eigenfunction analysis , normalized reaction diffusion , solitons
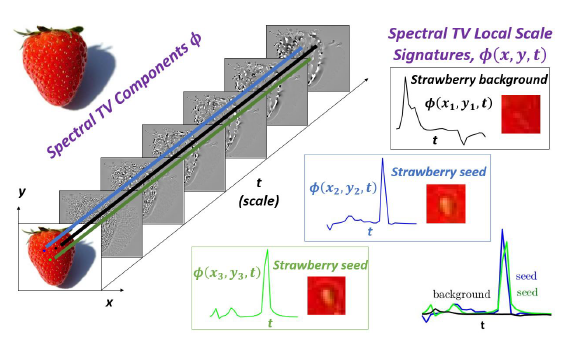
Spectral Total-Variation Local Scale Signatures for Image Manipulation and Fusion
We propose a unified framework for isolating, comparing and differentiating objects within an image. We rely on the recently proposed total-variation transform, yielding a continuous, multi-scale, fully edge-preserving, local descriptor, referred to as spectral total-variation local scale signatures. We show and analyze several useful merits of this framework. Signatures are sensitive to size, local contrast and composition of structures; are invariant to translation, rotation, flip and linear illumination changes; and texture signatures are robust to the underlying structures. We prove exact conditions in the 1D case. We propose several applications for this framework: saliency map extraction for fusion of thermal and optical images or for medical imaging, clustering of vein-like features and size-based image manipulation.

New Book
Many thanks to the whole group for contributing, commenting and proof-reading the new book.

Theoretical Analysis of Flows Estimating Eigenfunctions of One-homogeneous Functionals
Jean-Francois Aujol, Guy Gilboa, Nicolas Papadakis, “Theoretical Analysis of Flows Estimating Eigenfunctions of One-homogeneous Functionals”, accepted to SIAM J. on Imaging Sciences.
Nonlinear eigenfunctions, induced by subgradients of one-homogeneous functionals (such as the 1-Laplacian), have shown to be instrumental in segmentation, clustering and image decomposition. We present a class of ows for nding such eigenfunctions, generalizing a method recently suggested by Nossek and Gilboa. We analyze the ows on grids and graphs in the time-continuous and timediscrete settings. For a specic type of ow within this class, we prove convergence of the numerical iterations procedure and prove existence and uniqueness of the time-continuous case. Several toy examples are provided for illustrating the theoretical results, showing how such ows can be used on images and graphs.
Tags: flows , nonlinear eigenfunctions , TV
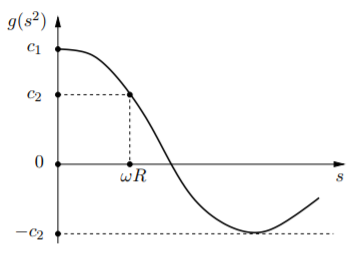
A Discrete Theory and Efficient Algorithms for Forward-and-Backward Diffusion Filtering
Martin Welk, Joachim Weickert, Guy Gilboa, “A Discrete Theory and Efficient Algorithms for Forward-and-Backward Diffusion Filtering”, preprint.
Image enhancement with forward-and-backward (FAB) diffusion lacks a sound theory and is numerically very challenging due to its diffusivities that are negative within a certain gradient range. In our paper we address both problems. First we establish a comprehensive theory for space-discrete and time-continuous FAB diffusion processes. It requires approximating the gradient magnitude with a nonstandard discretisation. Then we show that this theory carries over to the fully discrete case, when an explicit time discretisation with a fairly restrictive step size limit is applied.
To come up with more efficient algorithms we propose three
accelerated schemes:
(i) an explicit scheme with global time step size adaptation that is
also well-suited for parallel implementations on GPUs,
(ii) a randomised two-pixel scheme that offers optimal adaptivity of
the time step size,
(iii) a deterministic two-pixel scheme which benefits from less restrictive
consistency bounds.
Our experiments demonstrate that these algorithms allow speed-ups by up to three orders of magnitude without compromising stability or introducing visual artifacts.
Tags: discrete scheme , FAB , nonlinear diffusion

