G. Gilboa, “A Total Variation Spectral Framework for Scale and Texture Analysis”, CCIT Report 833, 2013.

Abstract:

A new total variation (TV) spectral framework is presented. A TV transform is proposed which can be interpreted as a spectral domain, where elementary TV features, like disks, approach impulses. A reconstruction formula from the pectral to the spatial domain is given, allowing the design of new filters.The framework allows deeper understanding of scales in an $L^1$ sense and the ability to better analyze and process textures. An example of a texture processing application illustrates possible benefits of this new framework.

G. Gilboa, “A spectral approach to total variation”, Scale-Space and Variational Methods, SSVM 2013, LNCS 7893, p. 36-47, 2013.

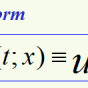
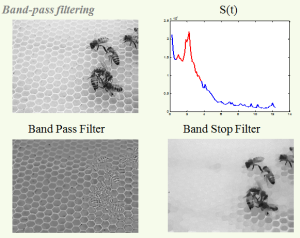
Abstract:

The total variation (TV) functional is explored from a spectral perspective. We formulate a TV transform based on the second time derivative of the total variation flow, scaled by time. In the transformation domain disks yield impulse responses. This transformation can be viewed as a spectral domain, with somewhat similar intuition of classical Fourier analysis. A simple reconstruction formula from the TV spectral domain to the spatial domain is given. We can then design low-pass, high-pass and band-pass TV filters and obtain a TV spectrum of signals and images.

  Matlab Code

G. Gilboa, “Expert regularizers for task specific processing”, Scale-Space and Variational Methods, SSVM 2013, LNCS 7893, p. 24-35, 2013

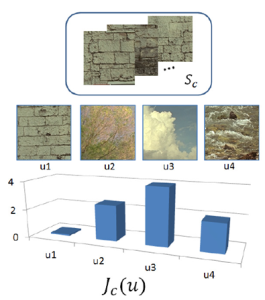
Abstract:

This study is concerned with constructing expert regularizers for specific tasks. We discuss the general problem of what is desired from a regularizer, when one knows the type of images to be processed. The aim is to improve the processing quality and to reduce artifacts created by standard, general-purpose, regularizers, such as total-variation or nonlocal functionals. Fundamental requirements for the theoretic expert regularizer are formulated. A simplistic regularizer is then presented, which approximates in some sense the ideal requirements.

G. Gilboa, S. Osher, “Nonlocal linear image regularization and supervised segmentation”, SIAM Multiscale Mod. Simul. (MMS), Vol. 6, No. 2, pp. 595-630, 2007.

Abstract

A nonlocal quadratic functional of weighted differences is examined. The weights are based on image features and represent the affinity between different pixels in the image. By prescribing different formulas for the weights, one can generalize many local and nonlocal linear denoising algorithms, including the nonlocal means filter and the bilateral filter. In this framework one can easily show that continuous iterations of the generalized filter obey certain global characteristics and converge to a constant solution. The linear
operator associated with the Euler-Lagrange equation of the functional is closely related to the graph Laplacian. We can thus interpret the steepest descent for minimizing the functional as a nonlocal diffusion process. This formulation allows a convenient framework for nonlocal variational minimizations, including variational denoising, Bregman iterations and the recently proposed inverse-scale-space.

It is also demonstrated how the steepest descent flow can be used for segmentation. Following kernel based methods in machine learning, the generalized diffusion process is used to propagate sporadic initial user’s information to the entire image. Unlike classical variational segmentation methods the process is not explicitly based on a curve length energy and thus can cope well with highly non-convex shapes and corners. Reasonable robustness to noise is still achieved.

 

  Matlab Code for non-local diffusion

Tags: NLH1 , Nonlocal diffusion , nonlocal regularizers

G. Gilboa, “Nonlinear Scale Space with Spatially Varying Stopping Time”, PAMI, Vol. 30, No. 12, pp. 2175-2187, 2008.

Abstract:

A general scale space algorithm is presented for denoising signals and images with spatially varying dominant scales. The process is formulated as a partial differential equation with spatially varying time. The proposed adaptivity is semi-local and is in conjunction with the classical gradient-based diffusion coefficient, designed to preserve edges. The new algorithm aims at maximizing a local SNR measure of the denoised image. It is based on a generalization of a global stopping time criterion presented recently by the author and colleagues. Most notably, the method works well also for partially textured images and outperforms any selection of a global stopping time. Given an estimate of the noise variance, the procedure is automatic and can be applied well to most natural images.

Tags: nonlinear diffusion , nonlinear scale-space , stopping time

G. Gilboa, N. Sochen, Y.Y. Zeevi, “Estimation of optimal PDE-based denoising in the SNR sense”, IEEE Trans. on Image Processing Vol. 15, No. 8, pp. 2269-2280, 2006.

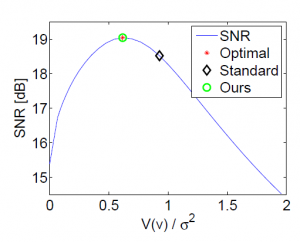
Abstract:

This paper is concerned with finding the best PDE-based denoising process, out of a set of possible ones. We focus either on finding the proper weight of the fidelity term in the energy minimization formulation, or on determining the optimal stopping time of a nonlinear diffusion process. A necessary condition for achieving maximal SNR is stated, based on the covariance of the noise and the residual part. We provide two practical alternatives for estimating this condition, by observing that the filtering of the image and the noise can be approximated by a decoupling technique, with respect to the weight or time parameters.

Our automatic algorithm obtains quite accurate results on a variety of synthetic and natural images, including piecewise smooth and textured ones. We assume that the statistics of the noise were previously estimated. No a-priori knowledge regarding the characteristics of the clean image is required .

A theoretical analysis is carried out, where several SNR performance bounds are established for the optimal strategy and for a widely used method, wherein the variance of the residual part equals the variance of the noise.

G. Gilboa, J. Darbon, S. Osher and T. Chan, Nonlocal Convex Functionals for Image Regularization. UCLA CAM Report 06-57

Abstract:

We examine weighted nonlocal convex functionals. The weights determine the affinities between different regions in the image and are computed according to image features. The L1 energy of this type can be viewed as a nonlocal extension of total-variation. Thus we obtain non-local versions of ROF, TV-flow, Bregman iterations and inverse-scale-
space (based on nonlocal ROF). Constructing the weights using patch distances, similarly to the nonlocal-means of Buades-Coll-Morel results in very robust and powerful regularizations. The flows and minimizations are computed efficiently by extending some recently proposed graph-cuts techniques. Numerical results which illustrate the performance of such models are presented.

Older papers will be uploaded within a few weeks