Jonathan Brokman, Itay Gershon, Omer Hofman, Guy Gilboa, Roman Vainshtein
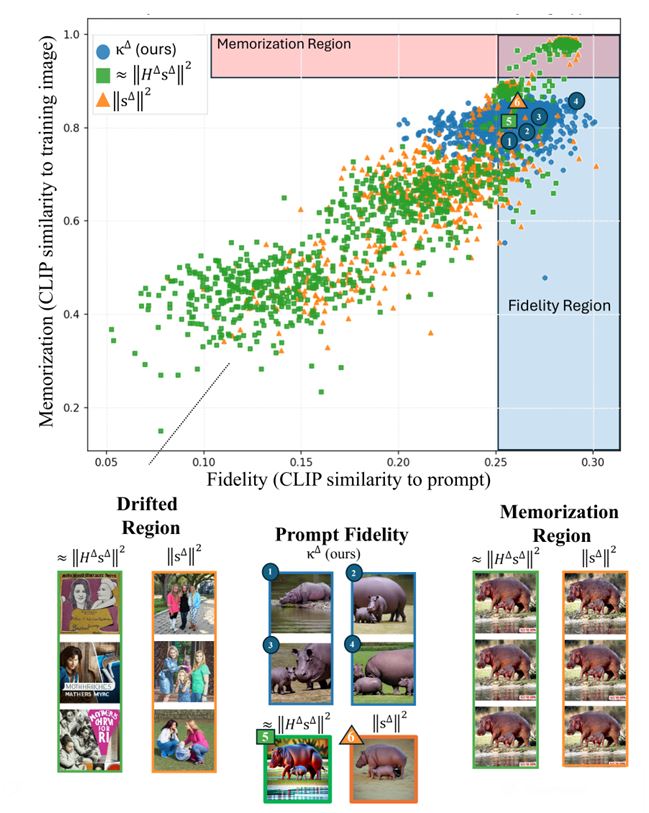
Memorization in generative text-to-image diffusion models is a phenomenon where instead of valid image generations, the model outputs near-verbatim reproductions of training images. This poses privacy and copyright risks, and remains difficult to prevent without harming prompt fidelity. We present a mid-generation, geometry-informed criterion that detects, and then helps avoid (mitigate), memorized outputs. Our method analyzes the natural image distribution manifold as learnt by the diffusion model. We analyze a memorization criterion that has a local curvature interpretation. Thus we can track the generative process, and our criterion’s trajectory throughout it, to understand typical geometrical structures traversed throughout this process. This is harnessed as a geometry-aware indicator that distinguishes memorized from valid generations. Notably, our criterion uses only the direction of the normalized score field, unlike prior magnitude-based methods; combining direction and magnitude we improve mid-generation detection SOTA by %. Beyond detecting memorization, we use this indicator as a plug-in to a mitigation policy to steer trajectories away from memorized basins while preserving alignment to the text. Empirically, this demonstrates improved fidelity–memorization trade-off over the competitors. By linking memorization to magnitude-invariant geometric signatures of the generative process, our work opens a new direction for understanding—and systematically mitigating—failure modes in diffusion models. Official code: https://bit.ly/4ndeISd