Category: Whats New

ICML 2025: Whitened CLIP as a Likelihood Surrogate of Images and Captions

Roy Betser, Meir-Yossef Levi, Guy Gilboa

Proceedings of the 42nd International Conference on Machine Learning (ICML), 2025

Likelihood approximations for images are not trivial to compute and can be useful in many applications. We examine the use of Contrastive Language-Image Pre-training (CLIP) to assess the likelihood of images and captions. We introduce \textit{Whitened CLIP}, a novel transformation of the CLIP latent space via an invertible linear operation. This transformation ensures that each feature in the embedding space has zero mean, unit standard deviation, and no correlation with all other features, resulting in an identity covariance matrix. We show that the whitened embeddings statistics can be well approximated as a standard normal distribution, thus, the log-likelihood is estimated simply by the square Euclidean norm in the whitened embedding space. The whitening procedure is completely training-free and performed using a pre-computed whitening matrix, hence, is very fast. We present several preliminary experiments demonstrating the properties and applicability of these likelihood scores to images and captions.

Camera ready version.

 

Code

ICML 2025: The Double-Ellipsoid Geometry of CLIP

Meir Yossef Levi, Guy Gilboa

Proceedings of the 42nd International Conference on Machine Learning (ICML), 2025

Contrastive Language-Image Pre-Training (CLIP) is highly instrumental in machine learning applications within a large variety of domains.
We investigate the geometry of this embedding, which is still not well understood, and show that text and image reside on linearly separable ellipsoid shells, not centered at the origin. We explain the benefits of having this structure, allowing to better embed instances according to their uncertainty during contrastive training.
Frequent concepts in the dataset yield more false negatives, inducing greater uncertainty.
A new notion of conformity is introduced, which measures the average cosine similarity of an instance to any other instance within a representative data set. We prove this measure can be accurately estimated by simply computing the cosine similarity to the modality mean vector. Furthermore, we find that CLIP’s modality gap optimizes the matching of the conformity distributions of image and text.

 

Camera ready paper

Code

Presenting at ICLR 2025

Nice trip to Singapore.

Omer and I presented our poster at ICLR 2025 on “Manifold Induced Biases for Zero-shot and Few-shot Detection of Generated Images” by

 Jonathan Brokman, Amit Giloni, Omer Hofman, Roman Vainshtein, Hisashi Kojima, Guy Gilboa.

 

Presenting poster at ICLR
Singapore sky line
Singapore boardwalk

ICLR 2025: Manifold Induced Biases for Zero-shot and Few-shot Detection of Generated Images

Jonathan Brokman · Amit Giloni · Omer Hofman · Roman Vainshtein · Hisashi Kojima · Guy Gilboa, ICLR 2025

Abatract:

Distinguishing between real and AI-generated images, commonly referred to as ‘image detection’, presents a timely and significant challenge. Despite extensive research in the (semi-)supervised regime, zero-shot and few-shot solutions have only recently emerged as promising alternatives. Their main advantage is in alleviating the ongoing data maintenance, which quickly becomes outdated due to advances in generative technologies. We identify two main gaps: (1) a lack of theoretical grounding for the methods, and (2) significant room for performance improvements in zero-shot and few-shot regimes. Our approach is founded on understanding and quantifying the biases inherent in generated content, where we use these quantities as criteria for characterizing generated images. Specifically, we explore the biases of the implicit probability manifold, captured by a pre-trained diffusion model. Through score-function analysis, we approximate the curvature, gradient, and bias towards points on the probability manifold, establishing criteria for detection in the zero-shot regime. We further extend our contribution to the few-shot setting by employing a mixture-of-experts methodology. Empirical results across 20 generative models demonstrate that our method outperforms current approaches in both zero-shot and few-shot settings. This work advances the theoretical understanding and practical usage of generated content biases through the lens of manifold analysis.

camera ready version

 

Code

 

SSVM 2025: Identifying Memorization of Diffusion Models through p-Laplace Analysis

Jonathan Brokman, Amit Giloni, Omer Hofman, Roman Vainshtein, Hisashi Kojima, and Guy Gilboa, Int. Conf. on Scale Space and Variational Methods, 2025

Abstract:

Diffusion models, today’s leading image generative models, estimate the score function, i.e. the gradient of the log probability of (perturbed) data samples, without direct access to the underlying probability distribution. This work investigates whether the estimated score function can be leveraged to compute higher-order differentials, namely p-Laplace operators. We show here these operators can be employed to identify memorized training data. We propose a numerical p-Laplace approximation based on the learned score functions, showing its effectiveness in identifying key features of the probability landscape. We analyze the structured case of Gaussian mixture models, and demonstrate the results carry-over to image generative models, where memorization identification based on the p-Laplace operator is performed for the first time.

JMIV 2024: Generalized Inversion of Nonlinear Operators

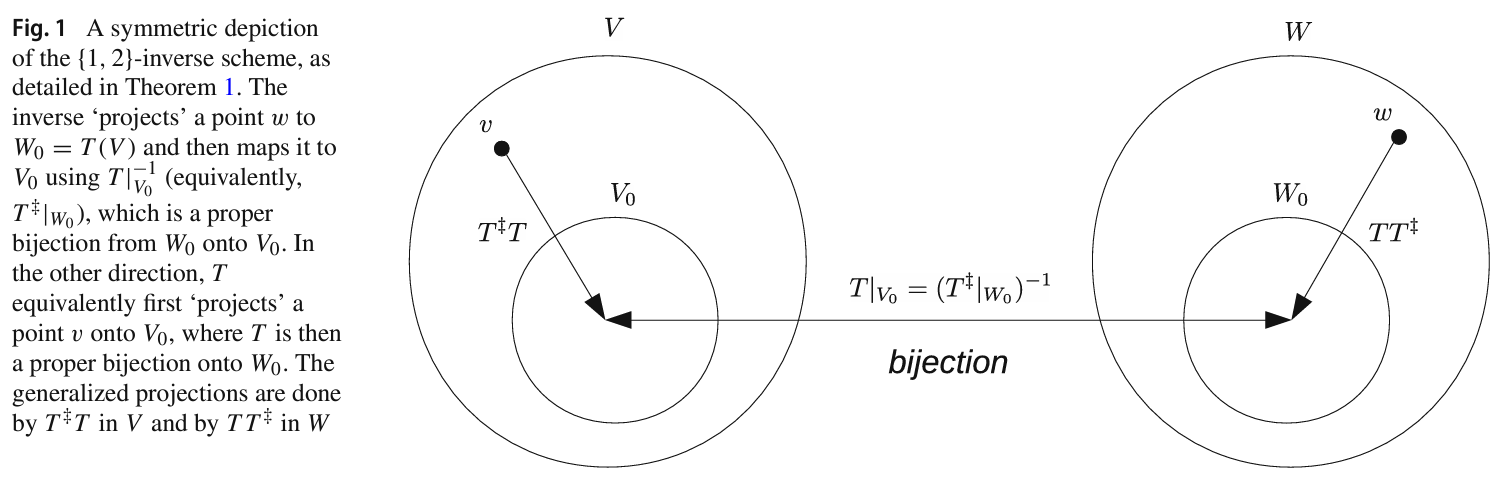
Eyal Gofer, Guy Gilboa, J. Mathematical Imaging and Vision (JMIV), 2024

Springer Open Access link

Inversion of operators is a fundamental concept in data processing. Inversion of linear operators is well studied, supported by established theory. When an inverse either does not exist or is not unique, generalized inverses are used. Most notable is the Moore–Penrose inverse, widely used in physics, statistics, and various fields of engineering. This work investigates generalized inversion of nonlinear operators. We first address broadly the desired properties of generalized inverses, guided by the Moore–Penrose axioms. We define the notion for general sets and then a refinement, termed pseudo-inverse, for normed spaces. We present conditions for existence and uniqueness of a pseudo-inverse and establish theoretical results investigating its properties, such as continuity, its value for operator compositions and projection operators, and others. Analytic expressions are given for the pseudo-inverse of some well-known, non-invertible, nonlinear operators, such as hard- or soft-thresholding and ReLU. We analyze a neural layer and discuss relations to wavelet thresholding. Next, the Drazin inverse, and a relaxation, are investigated for operators with equal domain and range. We present scenarios where inversion is expressible as a linear combination of forward applications of the operator. Such scenarios arise for classes of nonlinear operators with vanishing polynomials, similar to the minimal or characteristic polynomials for matrices. Inversion using forward applications may facilitate the development of new efficient algorithms for approximating generalized inversion of complex nonlinear operators.

 

ICLR 2024: Enhancing Neural Training via a Correlated Dynamics Model

Jonathan Brokman, Roy Betser, Rotem Turjeman, Tom Berkov, Ido Cohen, Guy Gilboa, ICLR 2024

Related preprint

As neural networks grow in scale, their training becomes both computationally demanding and rich in dynamics. Amidst the flourishing interest in these training dynamics, we present a novel observation: Parameters during training exhibit intrinsic correlations over time. Capitalizing on this, we introduce \emph{correlation mode decomposition} (CMD). This algorithm clusters the parameter space into groups, termed modes, that display synchronized behavior across epochs. This enables CMD to efficiently represent the training dynamics of complex networks, like ResNets and Transformers, using only a few modes. Moreover, test set generalization is enhanced.

We introduce an efficient CMD variant, designed to run concurrently with training. Our experiments indicate that CMD surpasses the state-of-the-art method for compactly modeled dynamics on image classification. Our modeling can improve training efficiency and lower communication overhead, as shown by our preliminary experiments in the context of federated learning.