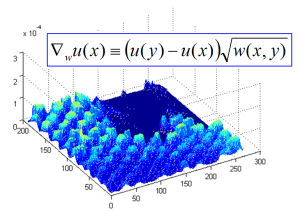
Processing image in a nonlocal manner using a variational approach. Nonlocal operators such as gradient and divergence are defined and used to form nonlocal functionals, such as nonlocal total variation (NLTV). Also evolution processes can be used (e.g. for denoising), for instance nonlocal diffusion. Segmentation, NL-TV-L1 and NL-TV-G minimizations are examined, as well as extensions of Chambolle’s projection algorithm to solve numerically the minimization problems.
Related papers (see PDF’s in publicaton part)
- J.-F. Aujol, G. Gilboa, N. Papadakis, “Non local total variation spectral framework”, Scale Space and Variational Methods in Computer Vision, SSVM 2015, LNCS 9087, p. 66-77, 2015.
- G. Gilboa, E. Appleboim, E. Saucan, Y.Y. Zeevi, “On the Role of Non-local Menger Curvature in Image Processing”, Proc. IEEE Int. Conf. Image Processing (ICIP), pp. 4337-4341, 2015. Recognized as part of the Top 10% papers in ICIP 2015.
- G. Gilboa, S. Osher, “Nonlocal Operators with Applications to Image Processing”, SIAM Multiscale Mod. Simul. (MMS), Vol. 7, No. 3, pp. 1005-1028, 2008.
- G. Gilboa, S. Osher, “Nonlocal linear image regularization and supervised segmentation”, SIAM Multiscale Mod. Simul. (MMS), Vol. 6, No. 2, pp. 595-630, 2007.
- G. Gilboa, S. Osher, “Nonlocal evolutions for image regularization”, Proc. SPIE Electronic Imaging, SPIE Vol. 6498, 64980U, 2007.
- G. Gilboa, J. Darbon, S. Osher and T. Chan, “Nonlocal Convex Functionals for Image Regularization“, UCLA CAM Report 06-57.