Semi-Inner-Products for Convex Functionals and Their Use in Image Decomposition

Abstract:

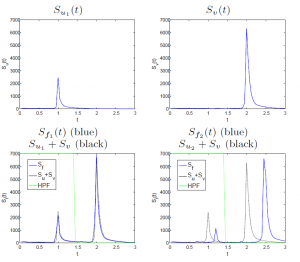
Semi-inner-products in the sense of Lumer are extended to convex functionals. This yields a Hilbert-space like structure to convex functionals in Banach spaces. In particular, a general expression for semi-inner-products with respect to one homogeneous functionals is given. Thus one can use the new operator for the analysis of total variation and higher order functionals like total-generalized-variation (TGV). Having a semi-inner-product, an angle between functions can be defined in a straightforward manner. It is shown that in the one homogeneous case the Bregman distance can be expressed in terms of this newly defined angle. In addition, properties of the semi-inner-product of nonlinear eigenfunctions induced by the functional are derived. We use this construction to state a sufficient condition for a perfect decomposition of two signals and suggest numerical measures which indicate when those conditions are approximately met.