J. of Mathematical Imaging and Vision (JMIV), Vol. 64, pp. 916–938, 2022.
Shai Biton and Guy Gilboa
Abstract
Our aim is to explain and characterize the behavior of adaptive total-variation (TV) regularization. TV has been widely used as an edge-preserving regularizer. However, objects are often over-regularized by TV, becoming blob-like convex structures of low curvature. This phenomenon was explained mathematically in the analysis of Andreau et al. They have shown that a TV regularizer can spatially preserve perfectly sets which are nonlinear eigenfunctions of the form $\lambda u \in \partial J_{TV}(u)$, where $\partial J_{TV}(u)$ is the TV subdifferential. For TV, these shapes are indeed convex sets of low-curvature.
A compelling approach to better preserve structures is to use adaptive anisotropic functionals, which adapt the regularization in an image-driven manner, with strong regularization along edges and low across them.
This follows the seminal work of Weickert on anisotropic diffusion. Adaptive anisotropic TV (A$^2$TV) was successfully used in several studies in the past decade. However, there is little analysis of the type of structures which can be well preserved. In this study we address this question by a joint methodology of mathematical derivations and experiments.
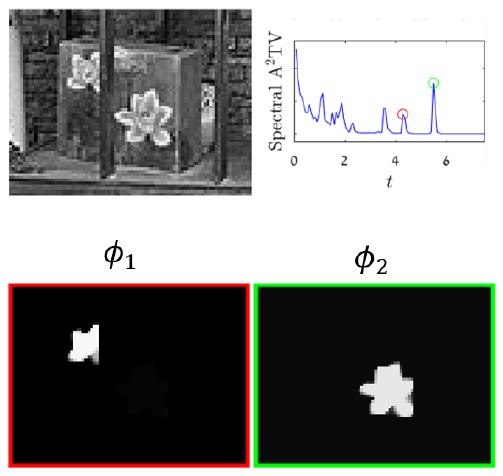
We rely on a recently developed theory of Burger et al on nonlinear spectral analysis of one-homogeneous functionals. We have that eigenfunction sets, admitting $\lambda u \in \partial J_{A^2TV}(u)$, are perfectly preserved under A$^2$TV-flow or minimization with $L^2$ square fidelity. We thus investigate these eigenfunctions theoretically and numerically. We prove non-convex sets can be eigenfunctions in certain conditions and provide numerical results which characterize well the relations between the degree of local anisotropy of the functional and the admitted maximal curvature. A nonlinear spectral representation is formulated, where shapes are well preserved and can be manipulated effectively. Finally, examples of possible applications related to shape manipulation and guided regularization of medical and depth data are shown.