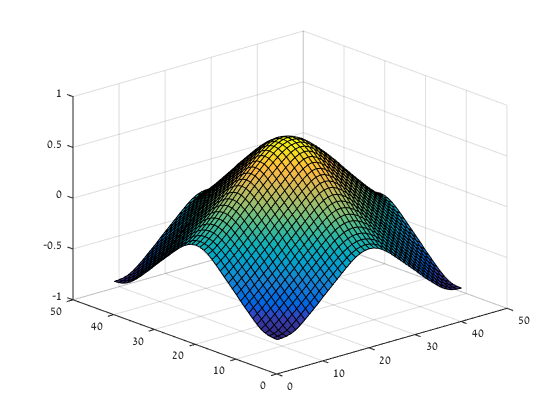
Flows Generating Nonlinear Eigenfunctions

Image above: Eigenfunction of TGV found by the proposed flow.

Abstract:

Nonlinear variational methods have become very powerful tools for many image processing tasks. Recently a new line of research has emerged, dealing with nonlinear eigenfunctions induced by convex functionals. This has provided new insights and better theoretical understanding of convex regularization and introduced new processing methods. However, the theory of nonlinear eigenvalue problems is still at its infancy. We present a new flow that can generate nonlinear eigenfunctions of the form $T(u)=\lambda u$, where $T(u)$ is a nonlinear operator and $\lambda \in \mathbb{R} $ is the eigenvalue. We develop the theory where $T(u)$ is a subgradient element of a regularizing one-homogeneous functional, such as total-variation (TV) or total-generalized-variation (TGV). We introduce two flows: a forward flow and an inverse flow; for which the steady state solution is a nonlinear eigenfunction. The forward flow monotonically smooths the solution (with respect to the regularizer) and simultaneously increases the $L^2$ norm. The inverse flow has the opposite characteristics. For both flows, the steady state depends on the initial condition, thus different initial conditions yield different eigenfunctions. This enables a deeper investigation into the space of nonlinear eigenfunctions, allowing to produce numerically diverse examples, which may be unknown yet. In addition we suggest an indicator to measure the affinity of a function to an eigenfunction and relate it to pseudo-eigenfunctions in the linear case