Ido Cohen, Tom Berkov, Guy Gilboa, “Total-Variation Mode Decomposition”, Proc. SSVM 2021, pp. 52-64
Abstract
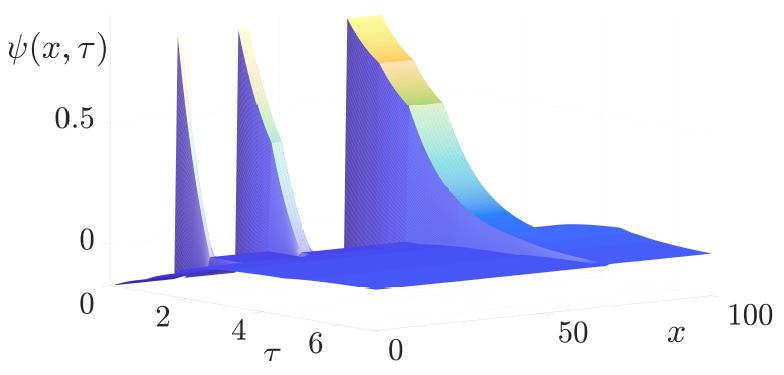
In this work we analyze the Total Variation (TV) flow applied to one dimensional signals. We formulate a relation between Dynamic Mode Decomposition (DMD), a dimensionality reduction method based on the Koopman operator, and the spectral TV decomposition. DMD is adapted by time rescaling to fit linearly decaying processes, such as the TV flow. For the flow with finite subgradient transitions, a closed form solution of the rescaled DMD is formulated. In addition, a solution to the TV-flow is presented, which relies only on the initial condition and its corresponding subgradient. A very fast numerical algorithm is obtained which solves the entire flow by elementary subgradient updates.
Bibtex Citation
@InProceedings{10.1007/978-3-030-75549-2_5,
author="Cohen, Ido
and Berkov, Tom
and Gilboa, Guy",
editor="Elmoataz, Abderrahim
and Fadili, Jalal
and Qu{\'e}au, Yvain
and Rabin, Julien
and Simon, Lo{\"i}c",
title="Total-Variation Mode Decomposition",
booktitle="Scale Space and Variational Methods in Computer Vision",
year="2021",
publisher="Springer International Publishing",
address="Cham",
pages="52--64",
}