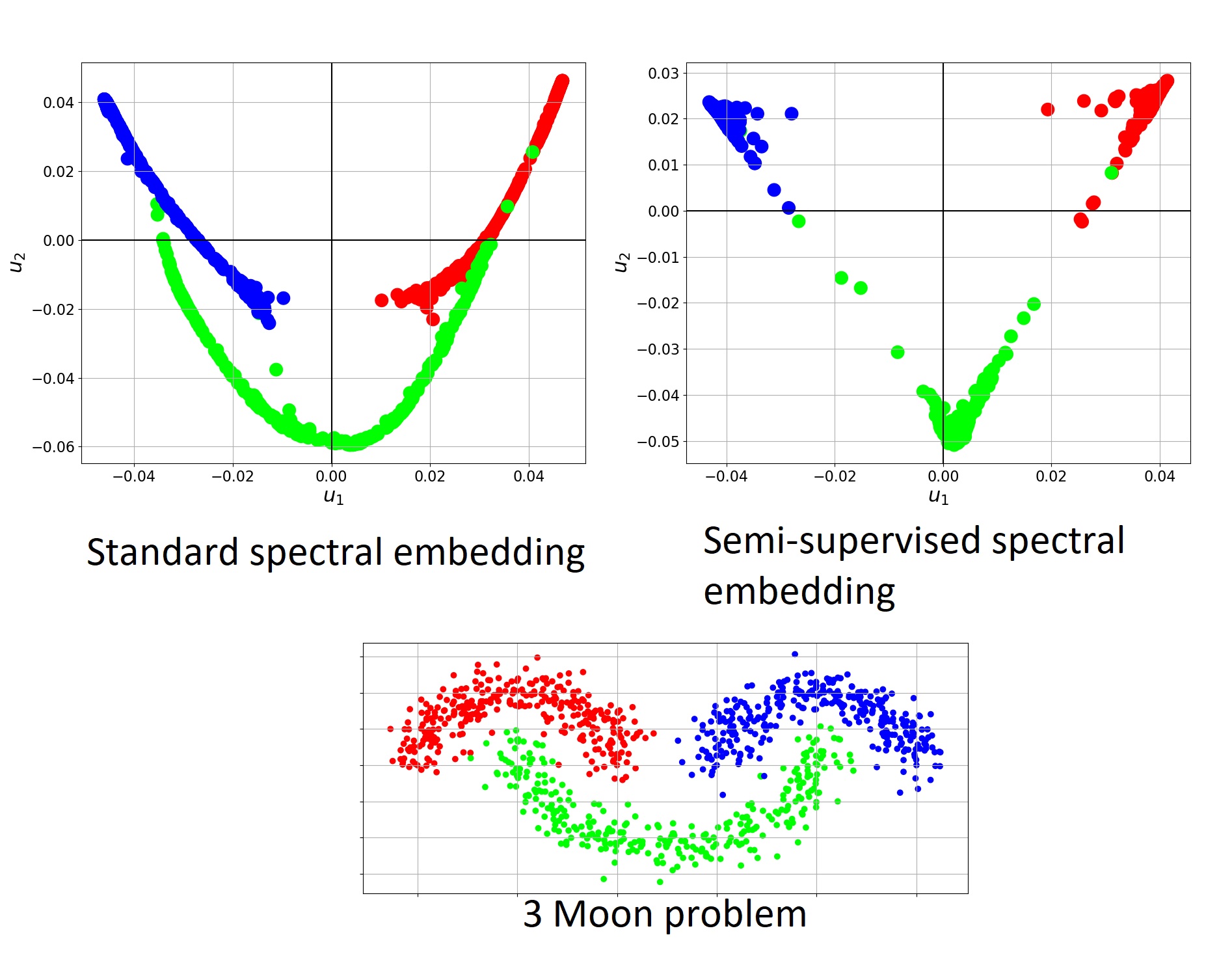
Summary
A new graph-Laplacian definition for the semi-supervised case which allows to perform better spectral clusterring, incorporating the labeled data in the eigenvectors.
Or Streicher, Guy Gilboa, accepted to SSVM 2023 (oral)
9th International Conference, SSVM 2023, Santa Margherita di Pula, Italy, May 21–25, 2023, Proceedings, Springer LNCS 14009, pp. 250-262, 2023.
Springer conference proceedings
Abatract
Semi-supervised learning is highly useful in common scenarios
where labeled data is scarce but unlabeled data is abundant. The
graph (or nonlocal) Laplacian is a fundamental smoothing operator for
solving various learning tasks. For unsupervised clustering, a spectral embedding
is often used, based on graph-Laplacian eigenvectors. For semisupervised
problems, the common approach is to solve a constrained
optimization problem, regularized by a Dirichlet energy, based on the
graph-Laplacian. However, as supervision decreases, Dirichlet optimization
becomes suboptimal. We therefore would like to obtain a smooth
transition between unsupervised clustering and low-supervised graphbased
classification.
In this paper, we propose a new type of graph-Laplacian which is adapted
for Semi-Supervised Learning (SSL) problems. It is based on both density
and contrastive measures and allows the encoding of the labeled data directly
in the operator. Thus, we can perform successfully semi-supervised
learning using spectral clustering. The benefits of our approach are illustrated
for several SSL problems.