for receiving her Ph.D.
Author: Guy Gilboa
Congrats to Reut Azaria!
for receiving her MSc
Total-Variation – Fast Gradient Flow and Relations to Koopman Theory
Ido Cohen, Tom Berkov, arXiv preprint
Abstract
The space-discrete Total Variation (TV) flow is analyzed using several mode decomposition techniques. In the one-dimensional case, we provide analytic formulations to Dynamic Mode Decomposition (DMD) and to Koopman Mode Decomposition (KMD) of the TV-flow and compare the obtained modes to TV spectral decomposition. We propose a computationally efficient algorithm to evolve the one-dimensional TV-flow. A significant speedup by three orders of magnitude is obtained, compared to iterative minimizations. A common theme, for both mode analysis and fast algorithm, is the significance of phase transitions during the flow, in which the subgradient changes. We explain why applying DMD directly on TV-flow measurements cannot model the flow or extract modes well. We formulate a more general method for mode decomposition that coincides with the modes of KMD. This method is based on the linear decay profile, typical to TV-flow. These concepts are demonstrated through experiments, where additional extensions to the two-dimensional case are given.
PhIT-Net: Photo-consistent Image Transform for Robust Illumination Invariant Matching
The 32nd British Machine Vision Conference (BMVC), Nov. 2021.
Damian Kaliroff and Guy Gilboa
BMVC link to paper, video and code
Abstract
We propose a new and completely data-driven approach for generating a photo- consistent image transform. We show that simple classical algorithms which operate in the transform domain become extremely resilient to illumination changes. This considerably improves matching accuracy, outperforming the use of state-of-the-art invariant representations as well as new matching methods based on deep features. The transform is obtained by training a neural network with a specialized triplet loss, designed to emphasize actual scene changes while attenuating illumination changes. The transform yields an illumination invariant representation, structured as an image map, which is highly flexible and can be easily used for various tasks.
Adaptive LiDAR Sampling and Depth Completion using Ensemble Variance
Accepted to IEEE Trans. Image Processing, 2021.
Eyal Gofer, Shachar Praisler, Guy Gilboa, arXiv
Abstract
This work considers the problem of depth completion, with or without image data, where an algorithm may measure the depth of a prescribed limited number of pixels. The algorithmic challenge is to choose pixel positions strategically and dynamically to maximally reduce overall depth estimation error. This setting is realized in daytime or nighttime depth completion for autonomous vehicles with a programmable LiDAR. Our method uses an ensemble of predictors to define a sampling probability over pixels. This probability is proportional to the variance of the predictions of ensemble members, thus highlighting pixels that are difficult to predict. By additionally proceeding in several prediction phases, we effectively reduce redundant sampling of similar pixels. Our ensemble-based method may be implemented using any depth-completion learning algorithm, such as a state-of-the-art neural network, treated as a black box. In particular, we also present a simple and effective Random Forest-based algorithm, and similarly use its internal ensemble in our design. We conduct experiments on the KITTI dataset, using the neural network algorithm of Ma et al. and our Random Forest based learner for implementing our method. The accuracy of both implementations exceeds the state of the art. Compared with a random or grid sampling pattern, our method allows a reduction by a factor of 4-10 in the number of measurements required to attain the same accuracy.
Examining the Limitations of Dynamic Mode Decomposition through Koopman Theory Analysis
Ido Cohen, Guy Gilboa, arXiv preprint 2107.07456, 2021
Abstract
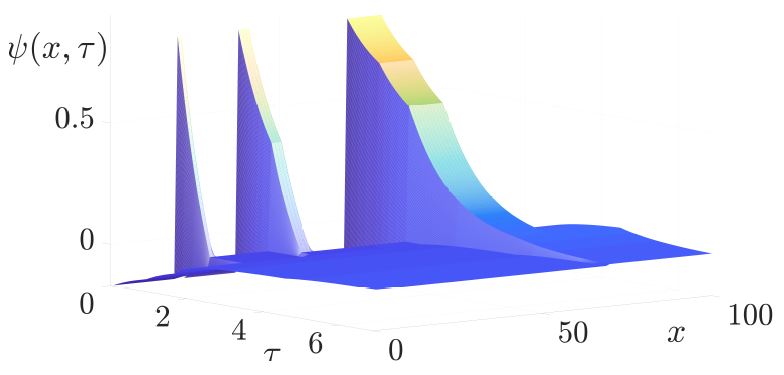
This work binds the existence of Koopman Eigenfunctions (KEF’s), the geometric of the dynamics, and the validity of Dynamic Mode Decomposition (DMD) to one coherent theory. Viewing the dynamic as a curve in the state-space allows us to formulate an existence condition of KEF’s and their multiplicities. These conditions lay the foundations for system reconstruction, global controllability, and observability for nonlinear dynamics.
DMD can be interpreted as a finite dimension approximation of Koopman Mode Decomposition (KMD). However, this method is limited to the case when KEF’s are linear combinations of the observations. We examine the limitations of DMD through the analysis of Koopman theory. We propose a new mode decomposition technique based on the typical time profile of the dynamics. An overcomplete dictionary of decay profiles is used to sparsely represent the dynamic. This analysis is also valid in the full continuous setting of Koopman theory, which is based on variational calculus.
We demonstrate applications of this analysis, such as finding KEF’s and their multiplicities, calculating KMD, dynamics reconstruction, global linearization, and controllability.
Total-Variation Mode Decomposition
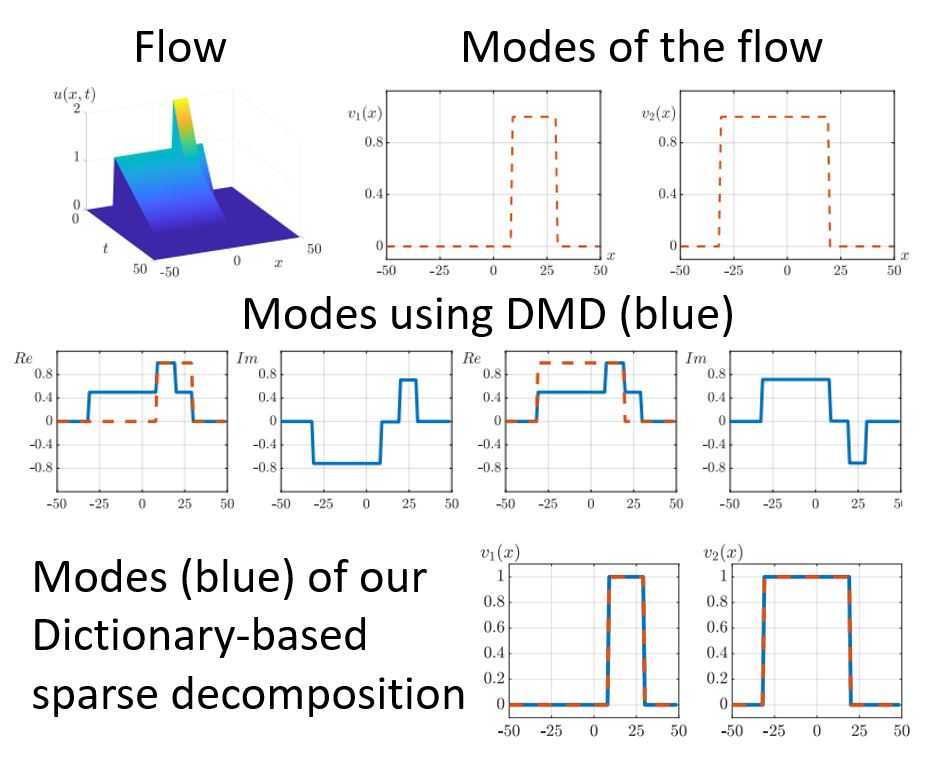
Ido Cohen, Tom Berkov, Guy Gilboa, “Total-Variation Mode Decomposition”, Proc. SSVM 2021, pp. 52-64
Abstract
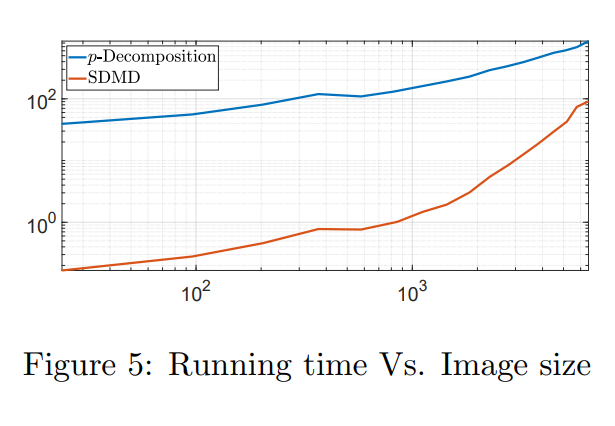
In this work we analyze the Total Variation (TV) flow applied to one dimensional signals. We formulate a relation between Dynamic Mode Decomposition (DMD), a dimensionality reduction method based on the Koopman operator, and the spectral TV decomposition. DMD is adapted by time rescaling to fit linearly decaying processes, such as the TV flow. For the flow with finite subgradient transitions, a closed form solution of the rescaled DMD is formulated. In addition, a solution to the TV-flow is presented, which relies only on the initial condition and its corresponding subgradient. A very fast numerical algorithm is obtained which solves the entire flow by elementary subgradient updates.
Bibtex Citation
@InProceedings{10.1007/978-3-030-75549-2_5,
author="Cohen, Ido
and Berkov, Tom
and Gilboa, Guy",
editor="Elmoataz, Abderrahim
and Fadili, Jalal
and Qu{\'e}au, Yvain
and Rabin, Julien
and Simon, Lo{\"i}c",
title="Total-Variation Mode Decomposition",
booktitle="Scale Space and Variational Methods in Computer Vision",
year="2021",
publisher="Springer International Publishing",
address="Cham",
pages="52--64",
}
Nonlinear Spectral Processing of Shapes via Zero-homogeneous Flows
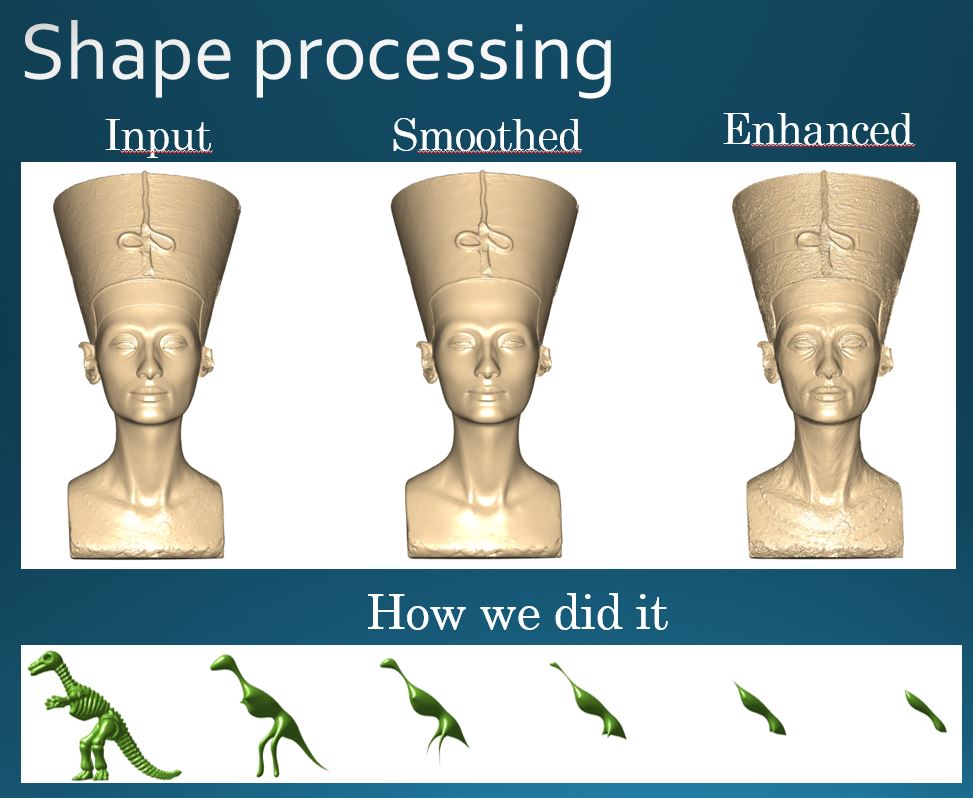
Abstract
In this work we extend the spectral total-variation framework, and use it to analyze and process 2D manifolds embedded in 3D. Analysis is performed in the embedding space – thus “spectral arithmetics” manipulate the shape directly. This makes our approach highly versatile and accurate for feature control. We propose three such methods, based on non-Euclidean zero-homogeneous p-Laplace operators. Each method satisfies distinct characteristics, demonstrated through smoothing, enhancing and exaggerating filters.
Cite
Brokman J., Gilboa G. (2021) Nonlinear Spectral Processing of Shapes via Zero-Homogeneous Flows. In: Elmoataz A., Fadili J., Quéau Y., Rabin J., Simon L. (eds) Scale Space and Variational Methods in Computer Vision. SSVM 2021. Lecture Notes in Computer Science, vol 12679. Springer, Cham. https://doi.org/10.1007/978-3-030-75549-2_4
Nonlinear Power Method for Computing Eigenvectors of Proximal Operators and Neural Networks
Accepted to SIAM J. on Imaging Scienes, 2021
Leon Bungert, Ester Hait-Fraenkel , Nicolas Papadakis and Guy Gilboa, arXiv
Neural networks have revolutionized the field of data science, yielding remarkable solutions in a data-driven manner. For instance, in the field of mathematical imaging, they have surpassed traditional methods based on convex regularization. However, a fundamental theory supporting the practical applications is still in the early stages of development. We take a fresh look at neural networks and examine them via nonlinear eigenvalue analysis. The field of nonlinear spectral theory is still emerging, providing insights about nonlinear operators and systems. In this paper we view a neural network as a complex nonlinear operator and attempt to find its nonlinear eigenvectors. We first discuss the existence of such eigenvectors and analyze the kernel of $\relu$ networks. Then we study a nonlinear power method for generic nonlinear operators. For proximal operators associated to absolutely one-homogeneous convex regularization functionals, we can prove convergence of the method to an eigenvector of the proximal operator. This motivates us to apply a nonlinear method to networks which are trained to act similarly as a proximal operator. In order to take the non-homogeneity of neural networks into account we define a modified version of the power method.
We perform extensive experiments on various shallow and deep neural networks designed for image denoising. For simple nets, we observe the influence of training data on the eigenvectors. For state-of-the-art denoising networks, we show that eigenvectors can be interpreted as (un)stable modes of the network, when contaminated with noise or other degradations.
Modes of Homogeneous Gradient Flows
Accepted to SIAM J. on Imaging Sciences, 2021
Ido Cohen, Omri Azencot, Pavel Lifshitz, Guy Gilboa, arXiv, July 2020
Finding latent structures in data is drawing increasing attention in broad and diverse fields such as fluid dynamics, signal processing, and machine learning. In this work, we formulate Dynamic Mode Decomposition (DMD) for two types of dynamical system. The first, a system which is derived by a $\gamma$-homogeneous operator ($\gamma\neq 1$).
The second, a system which can be represented as a symmetric operator.
Regarding to the first type, dynamical systems, derived by $\gamma$-homogeneous operators $\gamma\in[0,1)$, reach the steady state in finite time. This inherently contradicts the DMD model, which can be seen as an exponential data fitting algorithm. Therefore, the induced DMD operator leads to artifacts in the decomposition. We show certain cases where the DMD does not even exist. For homogeneous systems ($\gamma\neq 1$), we suggest a time rescaling that solves this conflict and show that DMD can perfectly restore the dynamics even for nonlinear flows. For dynamics which derived by a symmetric operator, we expect the eigenvalues of the DMD to be real. This requirement is embeded in a variant of the DMD algorithm, termed as Symmetric DMD (SDMD).
With these adaptations, we formulate a closed form solution of DMD for dynamics $u_t = P(u) $, $u(t=0)=u_0$, where $P$ is a nonlinear $\gamma$-homogeneous operator, when the initial condition $u_0$ admits the nonlinear eigenvalue problem $P(u_0)=\lambda u_0 $ ($u_0$ is a nonlinear eigenfunction, with respect to the operator $P$). We show experimentally that, for such systems, for any initial condition, SDMD achieves lower mean square error for the spectrum estimation. Finally, we formulate a discrete decomposition, related to nonlinear eigenfunctions of $\gamma$-homogeneous operator.