Category: Publications
CVPR 2026: The Universal Normal Embedding
C. Tasker, R. Betser, E. Gofer, M-Y Levi, G. Gilboa, CVPR 2026.
Generative models and vision encoders have largely advanced on separate tracks, optimized for different goals and grounded in different mathematical principles. Yet, they share a fundamental property: latent space Gaussianity. Generative models map Gaussian noise to images, while encoders map images to semantic embeddings whose coordinates empirically behave as Gaussian. We hypothesize that both are views of a shared latent source, the \emph{Universal Normal Embedding (UNE)}: an approximately Gaussian latent space from which encoder embeddings and DDIM-inverted noise arise as noisy linear projections. To test our hypothesis, we introduce \emph{NoiseZoo}, a dataset of per-image latents comprising DDIM-inverted diffusion noise and matching encoder representations (CLIP, DINO). On CelebA, linear probes in both spaces yield strong, aligned attribute predictions, indicating that generative noise encodes meaningful semantics along linear directions. These directions further enable faithful, controllable edits (e.g., smile, gender, age) without architectural changes, where simple orthogonalization mitigates spurious entanglements. Taken together, our results provide empirical support for the UNE hypothesis and reveal a shared Gaussian-like latent geometry that concretely links encoding and generation.
CVPR 2026: Training-free detection of generated videos via spatial-temporal likelihoods
O. Ben Hayun, R. Betser, M-Y Levi, L. Kassel, G. Gilboa, CVPR 2026.
Following major advances in text and image generation, the video domain has surged, producing highly realistic and controllable sequences that transform creative workflows. Along with this progress, these models also raise serious concerns about misinformation, making reliable detection of synthetic videos increasingly crucial. Image-based detectors are fundamentally limited because they operate per frame and ignore temporal dynamics, while supervised video detectors generalize poorly to unseen generators, a critical drawback given the rapid emergence of new models.These challenges motivate zero-shot approaches, which avoid synthetic data and instead score content against real-data statistics, enabling training-free, model-agnostic detection.
We introduce STALL, a simple, training-free, theoretically justified detector that provides likelihood-based scoring for videos, jointly modeling spatial and temporal evidence within a probabilistic framework. Across two public benchmarks including 20 generative models, STALL consistently outperforms prior image- and video-based baselines. To further test generalization, we curate ComGenVid, a new benchmark featuring state-of-the-art models (Sora and Veo-3), on which STALL demonstrates consistent and robust results.
CVPR 2026: Make it SING: Analyzing semantic invariants in classifiers
H. Yadid, M-Y Levi, R. Betser, G. Gilboa, CVPR 2026
All classifiers, including state-of-the-art vision models, possess invariants, partially rooted in the geometry of their linear mappings. These invariants, which reside in the null-space of the classifier, induce equivalent sets of inputs that map to identical outputs. The semantic content of these invariants remains vague, as existing approaches struggle to provide human-interpretable information. To address this gap, we present \emph{Semantic Interpretation of the Null-space Geometry} (SING), a method that constructs equivalent images, with respect to the network, and assigns semantic interpretations to the available variations. We use a mapping from network features to multi-modal vision language models. This allows us to obtain natural language descriptions and visual examples of the induced semantic shifts. SING can be applied to a single image, uncovering local invariants, or to sets of images, allowing a breadth of statistical analysis at the class and model levels. For example, our method reveals that ResNet50 leaks relevant semantic attributes to the null space, whereas DINO-ViT, a ViT pretrained with self-supervised DINO, is superior in maintaining class semantics across the invariant space.
ICLR 2026 (oral): InfoNCE Induces Gaussian Distribution
R. Betser, E. Gofer, M-Y Levi, G. Gilboa, ICLR 2026 (oral presentation, top 1.18%)
Contrastive learning has been at the bedrock of unsupervised learning in recent years, allowing training with massive unlabeled data for both task-specific and general (foundation) models. A prototypical loss in contrastive training is InfoNCE and its variants. In this paper we show that the embedding of the features which emerge from InfoNCE training can be well approximated by a multivariate Gaussian distribution. We justify this claim by taking two approaches. First, we show that under certain alignment and concentration assumptions, finite projections of a high dimensional representation approach multivariate Gaussian distribution, as the representation dimensions approach infinity.
Next, under less strict assumptions, we show that adding a small regularization term (which vanishes asymptotically) that promotes low feature norm and high feature entropy, we reach similar asymptotic results. We demonstrate experimentally, in a synthetic setting, CIFAR-10 and on pretrained foundation models, that the features indeed follow almost precise Gaussian distribution. One can use the Gaussian model to easily derive analytic expressions in the representation space and to obtain very useful measures, such as likelihood, data entropy and mutual information. Hence, we expect such theoretical grounding to be very useful in various applications involving contrastive learning.
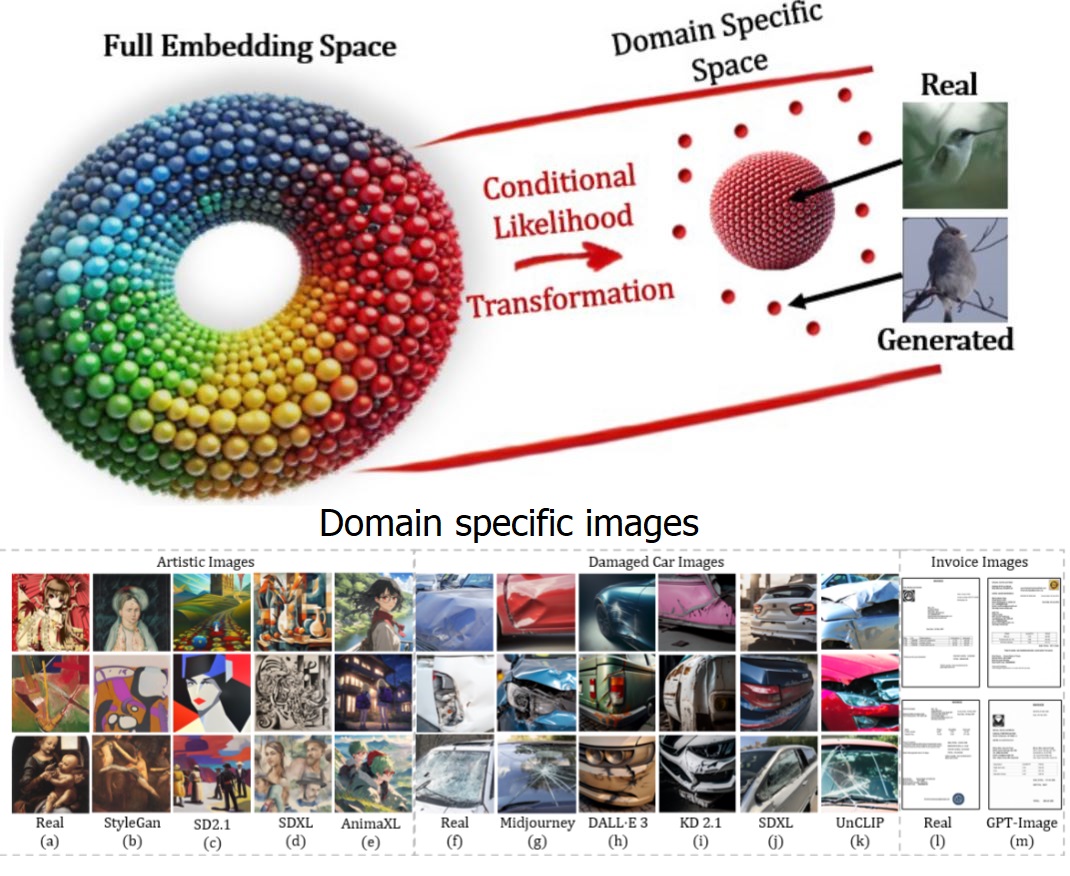
WACV 2026: General and Domain-Specific Zero-shot Detection of Generated Images via Conditional Likelihood
Roy Betser, Omer Hofman, Roman Vainshtein, Guy Gilboa, “General and Domain-Specific Zero-shot Detection of Generated Images via Conditional Likelihood”, accepted to Winter Conference on Applications of Computer Vision (WACV) 2026.
The rapid advancement of generative models, particularly diffusion-based methods, has significantly improved the realism of synthetic images. As new generative models continuously emerge, detecting generated images remains a critical challenge. While fully supervised, and few-shot methods have been proposed, maintaining an updated dataset is time-consuming and challenging. Consequently, zero-shot methods have gained increasing attention in recent years. We find that existing zero-shot methods often struggle to adapt to specific image domains, such as artistic images, limiting their real-world applicability. In this work, we introduce CLIDE, a novel zero-shot detection method based on conditional likelihood approximation. Our approach computes likelihoods conditioned on real images, enabling adaptation across diverse image domains. We extensively evaluate CLIDE, demonstrating state-of-the-art performance on a large-scale general dataset and significantly outperform existing methods in domain-specific cases. These results demonstrate the robustness of our method and underscore the need of broad, domain-aware generalization for the AI-generated image detection task.
The Visual Computer 2025: DXAI: Explaining Classification by Image Decomposition
Elnatan Kadar, Guy Gilboa, “DXAI: Explaining Classification by Image Decomposition”, accepted to The Visual Computer 2025.
We propose a new way to explain and to visualize neural network classification through a decomposition-based explainable AI (DXAI). Instead of providing an explanation heatmap, our method yields a decomposition of the image into class-agnostic and class-distinct parts, with respect to the data and chosen classifier. Following a fundamental signal processing paradigm of analysis and synthesis, the original image is the sum of the decomposed parts. We thus obtain a radically different way of explaining classification. The class-agnostic part ideally is composed of all image features which do not posses class information, where the class-distinct part is its complementary. This new visualization can be more helpful and informative in certain scenarios, especially when the attributes are dense, global and additive in nature, for instance, when colors or textures are essential for class distinction.
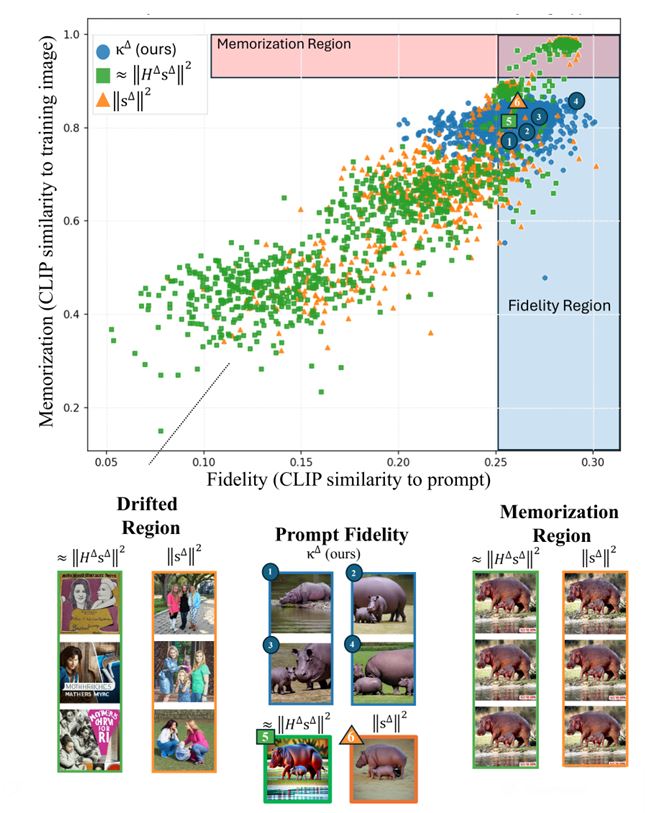
NeuReps 2025 (NeurIPS workshop): Tracking Memorization Geometry throughout the Diffusion Model Generative Process
Jonathan Brokman, Itay Gershon, Omer Hofman, Guy Gilboa, Roman Vainshtein
Memorization in generative text-to-image diffusion models is a phenomenon where instead of valid image generations, the model outputs near-verbatim reproductions of training images. This poses privacy and copyright risks, and remains difficult to prevent without harming prompt fidelity. We present a mid-generation, geometry-informed criterion that detects, and then helps avoid (mitigate), memorized outputs. Our method analyzes the natural image distribution manifold as learnt by the diffusion model. We analyze a memorization criterion that has a local curvature interpretation. Thus we can track the generative process, and our criterion’s trajectory throughout it, to understand typical geometrical structures traversed throughout this process. This is harnessed as a geometry-aware indicator that distinguishes memorized from valid generations. Notably, our criterion uses only the direction of the normalized score field, unlike prior magnitude-based methods; combining direction and magnitude we improve mid-generation detection SOTA by %. Beyond detecting memorization, we use this indicator as a plug-in to a mitigation policy to steer trajectories away from memorized basins while preserving alignment to the text. Empirically, this demonstrates improved fidelity–memorization trade-off over the competitors. By linking memorization to magnitude-invariant geometric signatures of the generative process, our work opens a new direction for understanding—and systematically mitigating—failure modes in diffusion models. Official code: https://bit.ly/4ndeISd
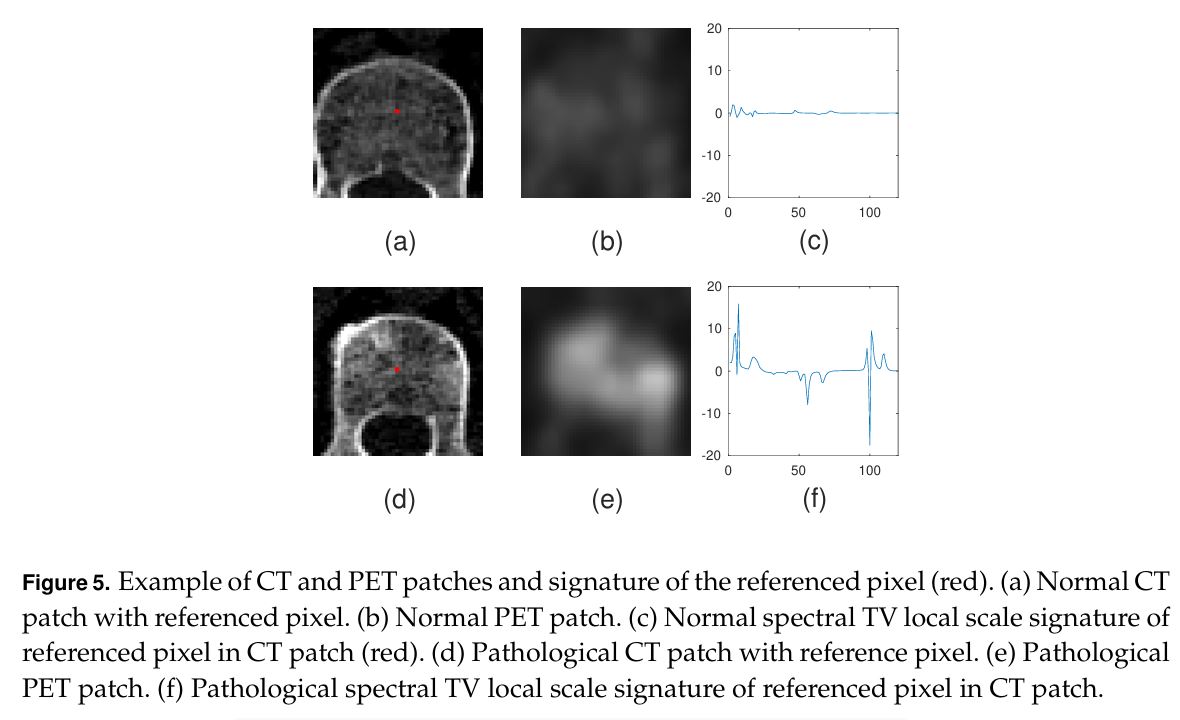
Philosophical Transactions A (2025): Ensemble of Weak Spectral Total Variation Learners: a PET-CT Case Study
Anna Rosenberg, John Kennedy, Zohar Keidar, Yehoshua Y. Zeevi and Guy Gilboa, Philosophical Transactions of the Royal Society A, 2025.
Abstract
Solving computer vision problems through machine learning, one often encounters lack of sufficient training data. To mitigate this, we propose the use of ensembles of weak learners based on spectral total-variation (STV) features (Gilboa G. 2014 A total variation spectral framework for scale and texture analysis. SIAM J. Imaging Sci. 7, 1937–1961. (doi:10.1137/130930704)). The features are related to nonlinear eigenfunctions of the total-variation subgradient and can characterize well textures at various scales. It was shown (Burger M, Gilboa G, Moeller M, Eckardt L, Cremers D. 2016 Spectral decompositions using one-homogeneous functionals. SIAM J. Imaging Sci. 9, 1374–1408. (doi:10.1137/15m1054687)) that, in the one-dimensional case, orthogonal features are generated, whereas in two dimensions the features are empirically lowly correlated. Ensemble learning theory advocates the use of lowly correlated weak learners. We thus propose here to design ensembles using learners based on STV features. To show the effectiveness of this paradigm, we examine a hard real-world medical imaging problem: the predictive value of computed tomography (CT) data for high uptake in positron emission tomography (PET) for patients suspected of skeletal metastases. The database consists of 457 scans with 1524 unique pairs of registered CT and PET slices. Our approach is compared with deep-learning methods and to radiomics features, showing STV learners perform best (AUC=0.87), compared with neural nets (AUC=0.75) and radiomics (AUC=0.79). We observe that fine STV scales in CT images are especially indicative of the presence of high uptake in PET.
ICML 2025: Whitened CLIP as a Likelihood Surrogate of Images and Captions
Roy Betser, Meir-Yossef Levi, Guy Gilboa
Proceedings of the 42nd International Conference on Machine Learning (ICML), 2025
Likelihood approximations for images are not trivial to compute and can be useful in many applications. We examine the use of Contrastive Language-Image Pre-training (CLIP) to assess the likelihood of images and captions. We introduce \textit{Whitened CLIP}, a novel transformation of the CLIP latent space via an invertible linear operation. This transformation ensures that each feature in the embedding space has zero mean, unit standard deviation, and no correlation with all other features, resulting in an identity covariance matrix. We show that the whitened embeddings statistics can be well approximated as a standard normal distribution, thus, the log-likelihood is estimated simply by the square Euclidean norm in the whitened embedding space. The whitening procedure is completely training-free and performed using a pre-computed whitening matrix, hence, is very fast. We present several preliminary experiments demonstrating the properties and applicability of these likelihood scores to images and captions.