Meir Yossef Levi, Guy Gilboa



Minimizing Quotient Regularization Model
Chao Wang, Jean-Francois Aujol, Guy Gilboa, Yifei Lou
Inverse Problems and Imaging 2024
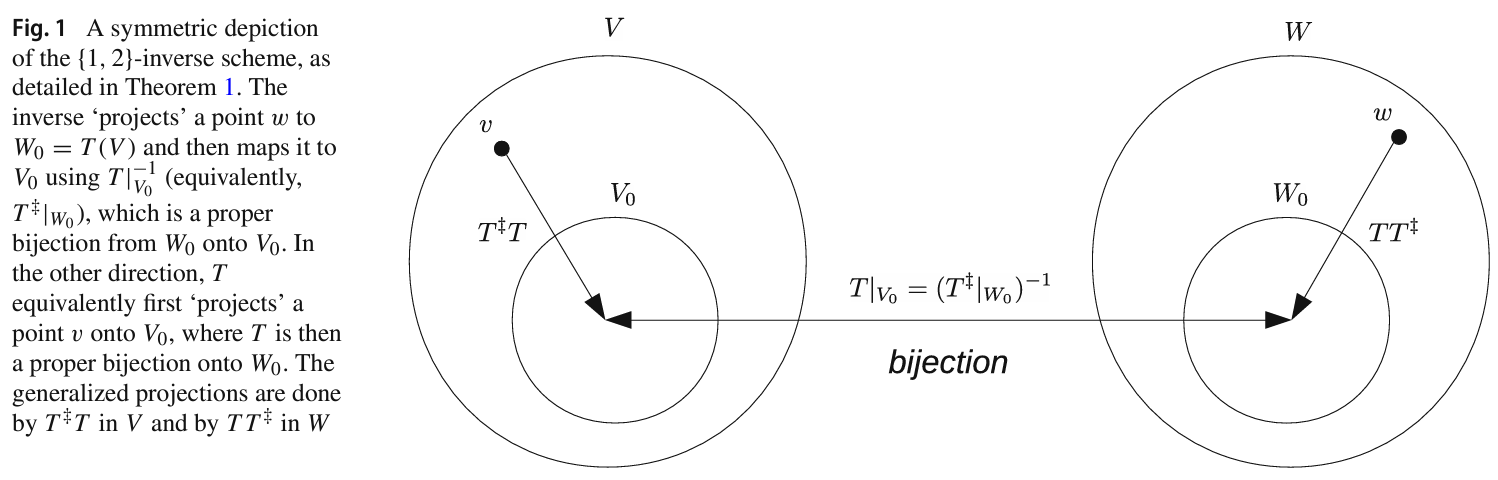
Eyal Gofer, Guy Gilboa, J. Mathematical Imaging and Vision (JMIV), 2024
Inversion of operators is a fundamental concept in data processing. Inversion of linear operators is well studied, supported by established theory. When an inverse either does not exist or is not unique, generalized inverses are used. Most notable is the Moore–Penrose inverse, widely used in physics, statistics, and various fields of engineering. This work investigates generalized inversion of nonlinear operators. We first address broadly the desired properties of generalized inverses, guided by the Moore–Penrose axioms. We define the notion for general sets and then a refinement, termed pseudo-inverse, for normed spaces. We present conditions for existence and uniqueness of a pseudo-inverse and establish theoretical results investigating its properties, such as continuity, its value for operator compositions and projection operators, and others. Analytic expressions are given for the pseudo-inverse of some well-known, non-invertible, nonlinear operators, such as hard- or soft-thresholding and ReLU. We analyze a neural layer and discuss relations to wavelet thresholding. Next, the Drazin inverse, and a relaxation, are investigated for operators with equal domain and range. We present scenarios where inversion is expressible as a linear combination of forward applications of the operator. Such scenarios arise for classes of nonlinear operators with vanishing polynomials, similar to the minimal or characteristic polynomials for matrices. Inversion using forward applications may facilitate the development of new efficient algorithms for approximating generalized inversion of complex nonlinear operators.
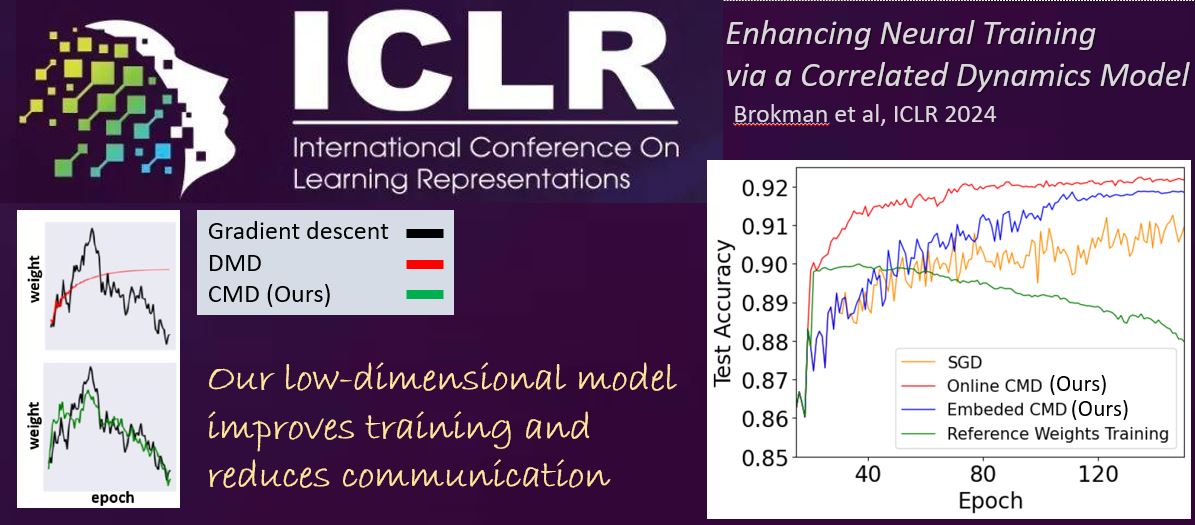
Jonathan Brokman, Roy Betser, Rotem Turjeman, Tom Berkov, Ido Cohen, Guy Gilboa, ICLR 2024
As neural networks grow in scale, their training becomes both computationally demanding and rich in dynamics. Amidst the flourishing interest in these training dynamics, we present a novel observation: Parameters during training exhibit intrinsic correlations over time. Capitalizing on this, we introduce \emph{correlation mode decomposition} (CMD). This algorithm clusters the parameter space into groups, termed modes, that display synchronized behavior across epochs. This enables CMD to efficiently represent the training dynamics of complex networks, like ResNets and Transformers, using only a few modes. Moreover, test set generalization is enhanced.
We introduce an efficient CMD variant, designed to run concurrently with training. Our experiments indicate that CMD surpasses the state-of-the-art method for compactly modeled dynamics on image classification. Our modeling can improve training efficiency and lower communication overhead, as shown by our preliminary experiments in the context of federated learning.

Jonathan Brokman, Martin Burger, Guy Gilboa, ACM Transactions on Graphics, 2024, https://doi.org/10.1145/3641845
We present an analysis of total-variation (TV) on non-Euclidean parameterized surfaces, a natural representation of the shapes used in 3D graphics. Our work explains recent experimental findings in shape spectral TV [Fumero et al., 2020] and adaptive anisotropic spectral TV [Biton and Gilboa, 2022]. A new way to generalize set convexity from the plane to surfaces is derived by characterizing the TV eigenfunctions on surfaces. Relationships between TV, area, eigenvalue, eigenfunctions and their discontinuities are discovered. Further, we expand the shape spectral TV toolkit to include versatile zero-homogeneous flows demonstrated through smoothing and exaggerating filters. Last but not least, we propose the first TV-based method for shape deformation, characterized by deformations along geometrical bottlenecks. We show these bottlenecks to be aligned with eigenfunction discontinuities. This research advances the field of spectral TV on surfaces and its application in 3D graphics, offering new perspectives for shape filtering and deformation.

Elnatan Kadar, Guy Gilboa
We propose a new way to explain and to visualize neural network classification through a decomposition-based explainable AI (DXAI). Instead of providing an explanation heatmap, our method yields a decomposition of the image into class-agnostic and class-distinct parts, with respect to the data and chosen classifier. Following a fundamental signal processing paradigm of analysis and synthesis, the original image is the sum of the decomposed parts. We thus obtain a radically different way of explaining classification. The class-agnostic part ideally is composed of all image features which do not posses class information, where the class-distinct part is its complementary. This new visualization can be more helpful and informative in certain scenarios, especially when the attributes are dense, global and additive in nature, for instance, when colors or textures are essential for class distinction.

Yossef Meir Levi, Guy Gilboa
The ability to cope accurately and fast with Out-Of-Distribution (OOD) samples is crucial in real-world safety demanding applications. In this work we first study the interplay between critical points of 3D point clouds and OOD samples. Our findings are that common corruptions and outliers are often interpreted as critical points. We generalize the notion of critical points into importance measures. We show that training a classification network based only on less important points dramatically improves robustness, at a cost of minor performance loss on the clean set. We observe that normalized entropy is highly informative for corruption analysis. An adaptive threshold based on normalized entropy is suggested for selecting the set of uncritical points. Our proposed importance measure is extremely fast to compute. We show it can be used for a variety of applications, such as Explainable AI (XAI), Outlier Removal, Uncertainty Estimation, Robust Classification and Adversarial Defense. We reach SOTA results on the two latter tasks.

Eyal Gofer, Guy Gilboa
Inversion of operators is a fundamental concept in data processing. Inversion of linear operators is well studied, supported by established theory. When an inverse either does not exist or is not unique, generalized inverses are used. Most notable is the Moore-Penrose inverse, widely used in physics, statistics, and various fields of engineering. This work investigates generalized inversion of nonlinear operators.
We first address broadly the desired properties of generalized inverses, guided by the Moore-Penrose axioms. We define the notion for general sets, and then a refinement, termed pseudo-inverse, for normed spaces. We present conditions for existence and uniqueness of a pseudo-inverse and establish theoretical results investigating its properties, such as continuity, its value for operator compositions and projection operators, and others. Analytic expressions are given for the pseudo-inverse of some well-known, non-invertible, nonlinear operators, such as hard- or soft-thresholding and ReLU. We analyze a neural layer and discuss relations to wavelet thresholding.
Next, the Drazin inverse, and a relaxation, are investigated for operators with equal domain and range. We present scenarios where inversion is expressible as a linear combination of forward applications of the operator. Such scenarios arise for classes of nonlinear operators with vanishing polynomials, similar to the minimal or characteristic polynomials for matrices. Inversion using forward applications may facilitate the development of new efficient algorithms for approximating generalized inversion of complex nonlinear operators.
Meir Yossef Levi, Guy Gilboa
Accepted to ICCV 2023.
Robust point cloud classification is crucial for real-world applications, as consumer-type 3D sensors often yield partial and noisy data, degraded by various artifacts. In this work we propose a general ensemble framework, based on partial point cloud sampling. Each ensemble member is exposed to only partial input data. Three sampling strategies are used jointly, two local ones, based on patches and curves, and a global one of random sampling. We demonstrate the robustness of our method to various local and global degradations. We show that our framework significantly improves the robustness of top classification netowrks by a large margin. Our experimental setting uses the recently introduced ModelNet-C database by Ren et al.[24], where we reach SOTA both on unaugmented and on augmented data. Our unaugmented mean Corruption Error (mCE) is 0.64 (current SOTA is 0.86) and 0.50 for augmented data (current SOTA is 0.57). We analyze and explain these remarkable results through diversity analysis.

Elnatan Kadar, Jonathan Brokman, Guy Gilboa
We present a new model, training procedure and architecture to create precise maps of distinction between two classes of images. The objective is to comprehend, in pixel-wise resolution, the unique characteristics of a class. These maps can facilitate self-supervised segmentation and objectdetection in addition to new capabilities in explainable AI (XAI). Our proposed architecture is based on image decomposition, where the output is the sum of multiple generative networks (branched-GANs). The distinction between classes is isolated in a dedicated branch. This approach allows clear, precise and interpretable visualization of the unique characteristics of each class. We show how our generic method can be used in several modalities for various tasks, such as MRI brain tumor extraction, isolating cars in aerial photography and obtaining feminine and masculine face features. This is a preliminary report of our initial findings and results.