Ido Cohen, Guy Gilboa, “Energy dissipating flows for solving nonlinear eigenpair problems”, Journal of Computational Physics 375 (2018), 1138-1158.
This work is concerned with computing nonlinear eigenpairs, which model solitary waves and various other physical phenomena. We aim at solving nonlinear eigenvalue problems of the general form
$T(u)=\lambda Q(u)$. In our setting $T$ is
a variational derivative of a convex functional (such as the Laplacian operator with respect to the Dirichlet energy),
$Q$ is an arbitrary bounded nonlinear operator and $\lambda$ is an unknown (real) eigenvalue.
We introduce a flow that numerically generates an eigenpair solution by its steady state.
Analysis for the general case is performed, showing a monotone decrease in the convex functional throughout the flow.
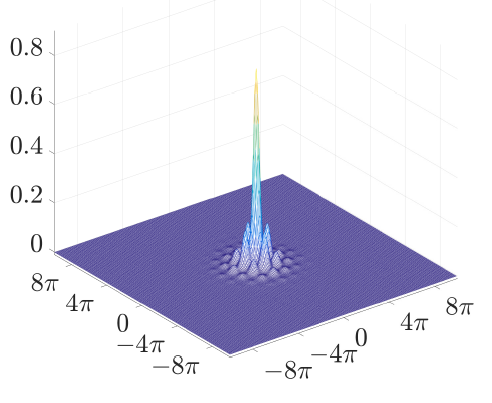
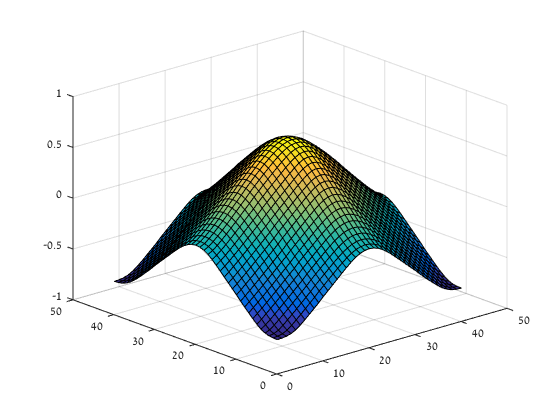
When $T$ is the Laplacian operator, a complete discretized version is presented and analyzed. We implement our algorithm on \ac{KdV} and \ac{NLS} equations in one and two dimensions.
The proposed approach is very general and can be applied to a large variety of models. Moreover, it is highly robust to noise and to perturbations in the initial conditions, compared to classical Petiashvili-based methods.
Tags: eigenpairs , nonlinear eigenfunction analysis , normalized reaction diffusion , solitons