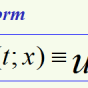G. Gilboa, “A Total Variation Spectral Framework for Scale and Texture Analysis”, SIAM Journal on Imaging Sciences, Vol. 7, No. 4, pp. 1937–1961, 2014.
Abstract:
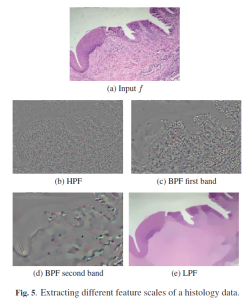
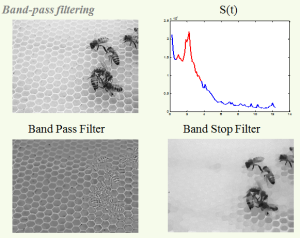
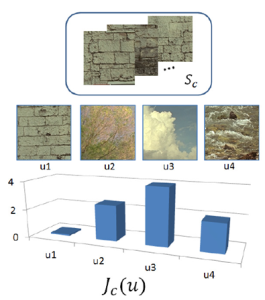
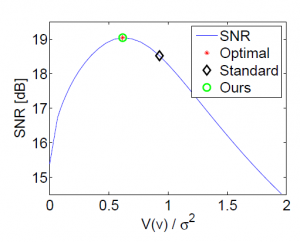
A new total variation (TV) spectral framework is presented. A TV transform is proposed which can be interpreted as a spectral domain, where elementary TV features, like disks, approach impulses. A reconstruction formula from the pectral to the spatial domain is given, allowing the design of new filters. The framework formulates a new representation of images which can enhance the understanding of scales in the $L^1$ sense and improve the analysis and processing of textures. An example of a texture processing application illustrates possible benefits of this new framework.