Adam Wolff, Shachar Praisler, Ilya Tcenov and Guy Gilboa, “Super-Pixel Sampler – a Data-driven Approach for Depth Sampling and Reconstruction”, accepted to ICRA (Int. Conf. on Robotics and Automation) 2020.

Paper

See the video of our mechanical prototype

Abstract

Depth acquisition, based on active illumination, is essential for autonomous and robotic navigation. LiDARs (Light Detection And Ranging) with mechanical, fixed, sampling templates are commonly used in today’s autonomous vehicles. An emerging technology, based on solid-state depth sensors, with no mechanical parts, allows fast and adaptive scans.

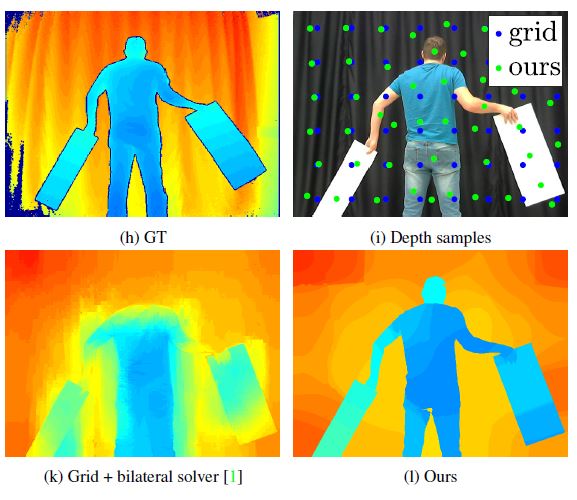
In this paper, we propose an adaptive, image-driven, fast, sampling and reconstruction strategy. First, we formulate a piece-wise planar depth model and estimate its validity for indoor and outdoor scenes. Our model and experiments predict that, in the optimal case, adaptive sampling strategies with about 20-60 piece-wise planar structures can approximate well a depth map. This translates to requiring a single depth sample for every 1200 RGB samples, providing strong motivation to investigate an adaptive framework. We propose a simple, generic, sampling and reconstruction algorithm, based on super-pixels. Our sampling improves grid and random sampling, consistently, for a wide variety of reconstruction methods. We propose an extremely simple and fast reconstruction for our sampler. It achieves state-of-the-art results, compared to complex image-guided depth completion algorithms, reducing the required sampling rate by a factor of 3-4.
A single-pixel depth camera built in our lab illustrates the concept.

Damian Kaliroff, Guy Gilboa, arXiv

We propose a new and completely data-driven approach for generating an unconstrained illumination invariant representation of images. Our method trains a
neural network with a specialized triplet loss designed to emphasize actual scene
changes while downplaying changes in illumination. For this purpose we use the
BigTime image dataset, which contains static scenes acquired at different times.
We analyze the attributes of our representation, and show that it improves patch
matching and rigid registration over state-of-the-art illumination invariant representations.
We point out that the utility of our method is not restricted to handling
illumination invariance, and that it may be applied for generating representations
which are invariant to general types of nuisance, undesired, image variants.

Ido Cohen, Guy Gilboa, “Energy dissipating flows for solving nonlinear eigenpair problems”, Journal of Computational Physics 375 (2018), 1138-1158.

This work is concerned with computing nonlinear eigenpairs, which model solitary waves and various other physical phenomena. We aim at solving nonlinear eigenvalue problems of the general form
$T(u)=\lambda Q(u)$. In our setting $T$ is
a variational derivative of a convex functional (such as the Laplacian operator with respect to the Dirichlet energy),
$Q$ is an arbitrary bounded nonlinear operator and $\lambda$ is an unknown (real) eigenvalue.
We introduce a flow that numerically generates an eigenpair solution by its steady state.

Analysis for the general case is performed, showing a monotone decrease in the convex functional throughout the flow.
When $T$ is the Laplacian operator, a complete discretized version is presented and analyzed. We implement our algorithm on \ac{KdV} and \ac{NLS} equations in one and two dimensions.
The proposed approach is very general and can be applied to a large variety of models. Moreover, it is highly robust to noise and to perturbations in the initial conditions, compared to classical Petiashvili-based methods.

Tags: eigenpairs , nonlinear eigenfunction analysis , normalized reaction diffusion , solitons