A 4 year grant NoMADS, Nonlocal Methods for Arbitrary Data Sources, as part of the RISE program, started on March 2018.
Includes Collaboration between universities (Munster, Cambridge, UCLA, Bordeaux, Carnegie Mellon, Technion and more..) and industry.
The paper, based on the master thesis of Raz Nossek is now accepted (Sept 2017):
R. Nossek & G. Gilboa, “Flows generating nonlinear eigenfunctions”, Journal of Scientific Computing.
(a pdf of the accepted version will be published soon, see arXiv version)
Abstract:
Nonlinear variational methods have become very powerful tools for many image processing tasks. Recently a new line of research has emerged, dealing with nonlinear eigenfunctions induced by convex functionals. This has provided new insights and better theoretical understanding of convex regularization and introduced new processing methods. However, the theory of nonlinear eigenvalue problems is still at its infancy. We present a new flow that can generate nonlinear eigenfunctions of the form $T(u)=\lambda u$, where $T(u)$ is a nonlinear operator and $\lambda \in \mathbb{R} $ is the eigenvalue. We develop the theory where $T(u)$ is a subgradient element of a regularizing one-homogeneous functional, such as total-variation (TV) or total-generalized-variation (TGV). We introduce two flows: a forward flow and an inverse flow; for which the steady state solution is a nonlinear eigenfunction. The forward flow monotonically smooths the solution (with respect to the regularizer) and simultaneously increases the $L^2$ norm. The inverse flow has the opposite characteristics. For both flows, the steady state depends on the initial condition, thus different initial conditions yield different eigenfunctions. This enables a deeper investigation into the space of nonlinear eigenfunctions, allowing to produce numerically diverse examples, which may be unknown yet. In addition we suggest an indicator to measure the affinity of a function to an eigenfunction and relate it to pseudo-eigenfunctions in the linear case
Abstract:
We propose to combine semantic data and registration algorithms to solve various image processing problems such as denoising, super-resolution and color-correction.
It is shown how such new techniques can achieve significant quality enhancement, both visually and quantitatively, in the case of facial image enhancement. Our model assumes prior high quality data of the person to be processed, but no knowledge of the degradation model.
We try to overcome the classical processing limits by using semantically-aware patches, with adaptive size and location regions of coherent structure and context, as building blocks. The method is demonstrated on the problem of cellular photography enhancement of dark facial images for different identities, expressions and poses
A new framework is proposed for variational analysis and processing. It defines a functional-based nonlinear transform and inverse-transform. The framework is developed in the context of total-variation (TV), but it can be generalized to other functionals.
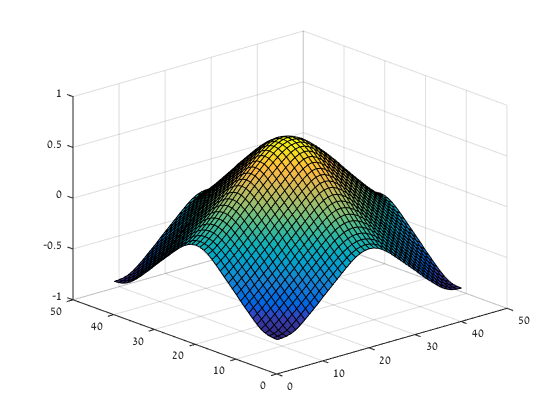
An eigenfunction, with respect to the subdifferential of the functional, such as a disk in the TV case, yields an impulse in the transform domain. This can be viewed as a generalization of known spectral approaches, based on linear algebra, which are extensively used in image-processing, e.g. for segmentation.
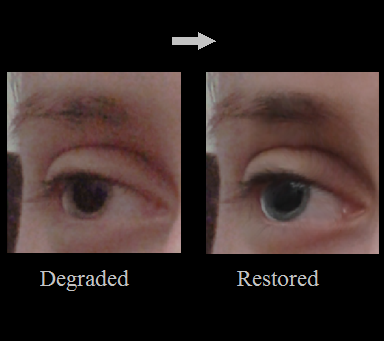
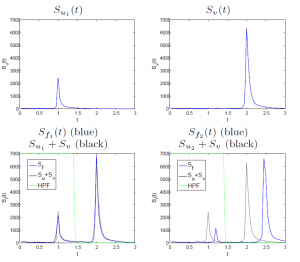
Following the Fourier intuition, a spectrum can be computed to analyze dominant scales in the image. Moreover, new nonlinear low-pass, high-pass and band-pass filters can be designed with full contrast and edge preservation.
Movie explained: Top (from left): image layers, phi bands (phi(t) = u_{tt}*t). Bottom: Ideal TV High-pass-filter, ideal TV Low-pass-filter at different scales. Ideal is in the sense of eigenfunctoin preservation.
Related papers
Ety’s paper in IEEE Trans. on Image Processing is published, “Blind Facial Image Quality Enhancement Using Non-Rigid Semantic Patches “.
Tal and Guy participated in a workshop in Cambridge (Newton Institute) on Variational methods, new optimisation techniques and new fast numerical algorithms.
Tal presented a poster on Spectral TV Hashing.
Guy presented a talk: Nonlinear spectral analysis – beyond the convex case
Abstract:
Semi-inner-products in the sense of Lumer are extended to convex functionals. This yields a Hilbert-space like structure to convex functionals in Banach spaces. In particular, a general expression for semi-inner-products with respect to one homogeneous functionals is given. Thus one can use the new operator for the analysis of total variation and higher order functionals like total-generalized-variation (TGV). Having a semi-inner-product, an angle between functions can be defined in a straightforward manner. It is shown that in the one homogeneous case the Bregman distance can be expressed in terms of this newly defined angle. In addition, properties of the semi-inner-product of nonlinear eigenfunctions induced by the functional are derived. We use this construction to state a sufficient condition for a perfect decomposition of two signals and suggest numerical measures which indicate when those conditions are approximately met.
Main topics
Complex diffusion real and imaginary kernels
Relaxed inverse scale space
Related papers
Abstract:
In this paper we demonstrate that the framework of nonlinear spectral decompositions based on total variation (TV) regularization is very well suited for image fusion as well as more general image manipulation tasks. The well-localized and edge-preserving spectral TV decomposition allows to select frequencies of a certain image to transfer particular features, such as wrinkles in a face, from one image to another. We illustrate the effectiveness of the proposed approach in several numerical experiments, including a comparison to the competing techniques of Poisson image editing, linear osmosis, wavelet fusion and Laplacian pyramid fusion. We conclude that the proposed spectral TV image decomposition framework is a valuable tool for semi- and fully-automatic image editing and fusion.
